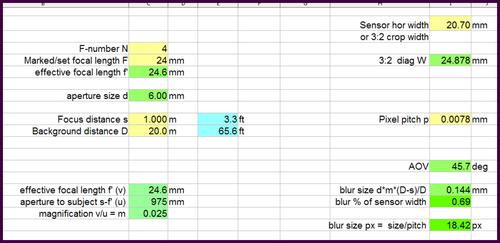
The size of out-of-focus blur can be measured directly by putting a ruler in the photograph so that it intersects the blur disc produced by a small point of light. The shot below was taken with a 25mm lens at f/1.4. The circular blur disc was from a small bright light over 10 metres away, while the camera was focussed on the ruler that was somewhere around the closest focus for that lens.
The scale on the ruler can then be used to measure the diameter of the blur disc in the plane of focus.
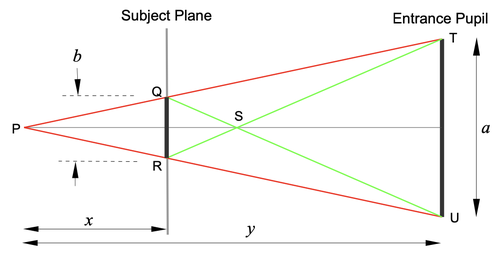
It is not difficult to calculate the size of the blur disc from a single point of light if the size of the entrance pupil is known, together with the distances of both the ruler and the point of light producing the blur (see this post in an earlier thread).
Alternative ways of measuring the size of the blur
The most obvious way is to measure the size of the blur in the image (measured in pixels) and then scale that to the size of the blur on the sensor (measured in mm). The size of the blur on the sensor will differ from the size of the blur in the plane of focus by the image magnification factor (for the plane of focus).
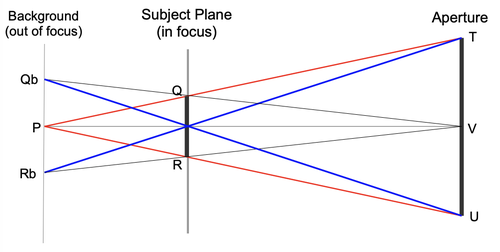
Merklinger, in his discussions of depth of field, gives a simple formula for the size of the blur in the plane of the object whose image was blurred. I'm not aware of any way this can be measured directly. I think it is probably a purely imaginary concept that is not open to direct measurement. Merklinger imagines how the appearance of the object is changed by being blurred and he imagines how the apparent size of the blurred object would compare to the size of the real object.
Note: I have started this thread as a result of a discussion in the thread on "Can I calculate focus distance from hyperfocal distance?"