Good information Tom, but can you please remove the word Bokeh from the title!?
Bokeh (as the term originally meant at least) is about the nature of out of focus highlights (smooth/hexagonal etc) not their size It is non quantitative.
Employing it as you have in the title encourages a misunderstanding of the term making it far less useful in discussions.
-
-
I can only agree, the term bokeh is constantly abused, to appear fashionable.
-
Thank you very much for your comments, which I appreciate.
I included "bokeh" in the title for a very pragmatic reason: to increase the chances of this thread being found by someone searching for phrases with "bokeh" in them. Online searches for, say, "how much bokeh" and "how much background blur" throw up completely different results. I wanted to cover both because I know that many beginning photographers do like to talk about "bokeh", even when they really should be saying "out-of-focus blur" or "background blur".
For this website to succeed, we need to have threads that are easily found by people searching online.
-
Well, the objection was to the way Bokeh and background blur are equated in your title. (I agree with the objection)
How about "Bokeh - and How much Background Blur will I Get?"
Rich
-
@TomAxford has written:
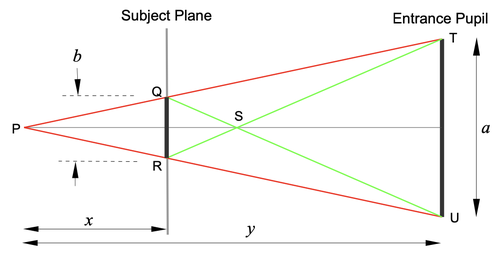
Calculating the size of the blur for any background (or foreground) distance
When light enters the lens, each different point on the surface of the lens "sees" the scene from a slightly different perspective. These slight differences in perspective cause objects that are not in the plane of focus to be blurred.
Consider the diagram below. Suppose that the camera is focussed on the subject (assumed to be in a plane) so that the sensor records a sharp image of the subject, but objects away from the subject plane will be blurred to a greater or lesser degree.
Point P is in the background. Consider how P is seen relative to the subject, when viewed from the entrance pupil of the lens. Seen from point T, P is in line with Q. Seen from point U, P is in line with R. From intermediate positions across the entrance pupil, P is in line with points in between Q and R.
When all those views are combined together, the point P appears as a blur, which extends from Q to R. So the distance from Q to R (labelled b in the diagram) is the diameter of the blur disk produced by a small bright light at point P.
A similar thing happens with the point S in the foreground. Viewed from T, S is in line with R. Viewed from U, S is in line with Q. So in the integrated view seen by the whole entrance pupil, S appears as a blur from Q to R.
It is a matter of simple geometry to work out the size of the blur in terms of the distances x and y:
b = ax/y
where:
b is the diameter of the blur in the subject plane,
a is the diameter of the entrance pupil,
x is the distance from point P to the subject plane,
y is the distance from point P to the entrance pupil.The same formula applies whether P is in the background or in the foreground.
As this is "beginners questions": I'd simply say:
- Open up your lens to its largest aperture.
- For maximum background blur (bokeh) get close to your subject and maximise the distance to the scenery behind them.
- Go out and shoot. ;-)
-
@BurnImage has written:
As this is "beginners questions": I'd simply say:
-
Open up your lens to its largest aperture.
-
For maximum background blur (bokeh) get close to your subject and maximise the distance to scenery behind them.
-
Go out and shoot. ;-)
Perhaps accompanied by a series of three images — three versions of the same scene — that illustrate the points. But very much this, without the diagram to consider.
-
-
@jaberg has written:@BurnImage has written:
As this is "beginners questions": I'd simply say:
-
Open up your lens to its largest aperture.
-
For maximum background blur (bokeh) get close to your subject and maximise the distance to scenery behind them.
-
Go out and shoot. ;-)
Perhaps accompanied by a series of three images — three versions of the same scene — that illustrate the points. But very much this, without the diagram to consider.
A series of images is the way to go for sure :)
-
-
@jaberg has written:@BurnImage has written:
As this is "beginners questions": I'd simply say:
-
Open up your lens to its largest aperture.
-
For maximum background blur (bokeh) get close to your subject and maximise the distance to scenery behind them.
-
Go out and shoot. ;-)
Perhaps accompanied by a series of three images — three versions of the same scene — that illustrate the points. But very much this, without the diagram to consider.
There are some beginners at photography who are comfortable with some mathematics. I like to cater for those people.
Also, there are probably people who are experienced photographers but who would like to understand more of the mathematics of background blur. I would not wish to insult them by calling them beginners, but they may still read Beginners' Questions. When I first joined DPReview, I used to read Beginners' Questions in the hope of learning something new (and I often did learn something that was new to me).
Anyone who is confused can always ask a question themselves either by starting a new thread or by posting a question in this thread.
-
-
@Rich42 has written:
Well, the objection was to the way Bokeh and background blur are equated in your title. (I agree with the objection)
How about "Bokeh - and How much Background Blur will I Get?"
Rich
I should think that would work the same with search engines
-
@Rich42 has written:
How about "Bokeh - and How much Background Blur will I Get?"
Thanks, I like that. I'll wait till tomorrow and if I still think the same I will change it.
-
@jaberg has written:@BurnImage has written:
As this is "beginners questions": I'd simply say:
-
Open up your lens to its largest aperture.
-
For maximum background blur (bokeh) get close to your subject and maximise the distance to scenery behind them.
-
Go out and shoot. ;-)
Perhaps accompanied by a series of three images — three versions of the same scene — that illustrate the points. But very much this, without the diagram to consider.
One way to think about it is photographing a vertical ruler with a bright, distant star off to the side of the ruler. You focus on the ruler at several distances from the camera, and the magnification of the ruler changes, and the size of the OOF star in the image, as measured by the ruler in the image, is always the size of the pupil, So, the closer the pupil is to the ruler, the larger both the ruler and OOF "disk" or "ball" are.
Of course, if you actually did this as a demonstration, you would need to have very little illumination on the ruler and a very high ISO exposure index to see the star spread out so thin when severely OOF.
-
-
@JohnSheehyRev has written:
One way to think about it is photographing a vertical ruler with a bright, distant star off to the side of the ruler. You focus on the ruler at several distances from the camera, and the magnification of the ruler changes, and the size of the OOF star in the image, as measured by the ruler in the image, is always the size of the pupil, So, the closer the pupil is to the ruler, the larger both the ruler and OOF "disk" or "ball" are.
Of course, if you actually did this as a demonstration, you would need to have very little illumination on the ruler and a very high ISO exposure index to see the star spread out so thin when severely OOF.
Yes, it is instructive to do experiments like that to measure the size of the blur.
It's easier to use a small bright light instead of a star. The image below used a small LED torch (with the reflector removed) about 15 metres away. The ruler was taped to a window. The entrance pupil was nominally 25/1.4=18mm.
-
Okay
. -
I am not sure why the size of the blur needs to be measured with a ruler. The only important thing is whether the effect gives approval or pleasure, though I must admit that the presence of absence of "bokeh", or whatever you want to call it, is not something that I personally worry about. I mean, surely the subject of the photo, which is presumably in focus, is the important thing, and I dont want the background to upstage it.
David
-
@davidwien has written:
I am not sure why the size of the blur needs to be measured with a ruler. The only important thing is whether the effect gives approval or pleasure, though I must admit that the presence of absence of "bokeh", or whatever you want to call it, is not something that I personally worry about. I mean, surely the subject of the photo, which is presumably in focus, is the important thing, and I dont want the background to upstage it.
David
A larger background blur is often desired precisely because the photographer doesn't want the background to compete with the subject for attention. The ruler demonstrates and verifies the principle of what determines OOF blur size; it is not about photographing rulers.
-
For me, the background is as important as the subject itself, and I always pay great attention to it.
-
In a few words: bigger is better!
-
@davidwien has written:
I am not sure why the size of the blur needs to be measured with a ruler.
Quite so. I prefer a little more accuracy in Open Office:
kronometric.org/phot/temp/blur%20dia.%20incl%20height.ods
Quoted message:The only important thing is whether the effect gives approval or pleasure, though I must admit that the presence or absence of "bokeh", or whatever you want to call it, is not something that I personally worry about. I mean, surely the subject of the photo, which is presumably in focus, is the important thing, and I dont want the background to upstage it.
bokeh, blur, or convolution is always present ... it is only absent in the focal plane and that only theoretically ... so you're right not to worry about it.
On the other hand, the degree of blur is a different matter: