[deleted]
-
-
Absolutely for the second bit, no for the first.
No, we don't. As I have said in far earlier posts there still seems to be a basic assumption you don't seem to be able to see beyond. A few posts ago you said:
None of the absolute mathematical relationships that you are treating as constant are actually perserved by the human visual system when you look at an image, or even the real world. And yet you are still treating the perspective you see in the image as an absolute truth and constant and assuming that there is no difference between the absolute linear geometry as rendered in the camera image and the assumed 3D perspective you see when you look at that image. It doesn't seem to occur to you to even question this.
Eye and Brain - R L Gregory:
"When an artist employs strict geometrical perspective he does not draw what he sees-he represents his retinal image. As we know these are very different; for what is seen is affected by constancy scaling. A photograph, on the other hand, represents the retinal image but not how the scene appears... ...The camera gives true geometrical perspective; but because we do not see the world as it is projected on the retina, or in the camera, the photograph looks wrong."
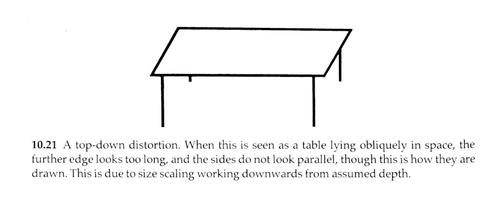
The front and back of our table here are exactly the same size, and so the two side are exactly parallel, and so the opposite angels are also exactly the same. This is the geometrical truth of the image and the truth of the photo and how it is mapped to the back of the retina.
But it is not what you see.
In fact very little of the geometry you actually see in the above image relates to it's true geometry. That the sides no longer look parallel is a clear indication that relative sizes as in the true geometry is not preserved in human vision. So:
Is proved to be incorrect as soon as we include human vision, the relationship is not maintained.
I keep saying that you can't relate what you see through human eyes directly to the geometry of image formation without taking into account the very nature of human perception because they are different. To fully understand telephoto compression it is necessary to fully understand the true nature of mathematically correct linear perspective and just how your view through human eyes differs from that. They are a long way from being one and the same.
P.s. I just posted an image and said the opposite, "it's not the same, see for yourself."
-
Maybe I misunderstand you, but IMO this is not geometrical truth of the image. You could get such image only by telecentric lens, which geometrically places center of perspective into (minus) infinity (in other words, makes focal length infinite). Using pinhole or any usual lens, you will get quite different image - sides not parallel and back side shorter.
-
It's not about how realistic the table is. This is highlighting a very real and observable difference between the pure and mathematically correct geometry as projected on the back of your retina and what you actually see. And to do this in a way that's obvious and uncluttered.
With the simple addition of legs the 2D shape transforms to a 3D understanding.
So if a 2D shape does have near and far sides that are the same length then as a 3D table top one must in reality be longer. And this is what the brain is doing, it scales up the further edge and changes the angle to fit (mathematical relationships are not preserved in human vision). In effect it is subtracting the distortion caused by perspective (viewing from a single point in space) and showing you the perceived true shape of the object.
I could do this with a the correct perspective for a rectangular table top, or indeed I could use the examples of the sugar bowl and mugs in my wide angle shot from my burger bar mentioned above. But the problem is that you would just assume that that correct perspective is directly linked to the correct maths of image geometry. You wouldn't even think to question it. By starting with a symmetrical shape that is easy to understand it's easy to show that distortion precisely because it goes against your expectation for the 3D table top.
The fact remains that the pure mathematical relationships of the object are not preserved by human vision, the angles and lengths are noticably different.
-
@Andrew564 has written:@ArvoJ has written:@Andrew564 has written:
The front and back of our table here are exactly the same size, and so the two side are exactly parallel, and so the opposite angels are also exactly the same. This is the geometrical truth of the image and the truth of the photo and how it is mapped to the back of the retina.
Maybe I misunderstand you, but IMO this is not geometrical truth of the image. You could get such image only by telecentric lens, which geometrically places center of perspective into (minus) infinity (in other words, makes focal length infinite). Using pinhole or any usual lens, you will get quite different image - sides not parallel and back side shorter.
It's not about how realistic the table is. This is highlighting a very real and observable difference between the pure and mathematically correct geometry as projected on the back of your retina and what you actually see. And to do this in a way that's obvious and uncluttered.
With the simple addition of legs the 2D shape transforms to a 3D understanding.
So I really misunderstood your text. Sorry, I can't always follow long passages :)
But your example is very good to show, how important context is. If I look at it as image of parallelogram with non-important additions, then it looks geometrically correct. If I look at it as image of table, then it is distorted.
I would classify this image as 'optical illusion', although telephoto compression could also considered as optical illusion.Back to perspective. I think that we see 'distortion' in the cases when we assume some distance to object and in reality it is taken from very different distance. (Same for object sizes.) Like full-size people images - we assume they have photographed from distance 3-6m (10-20ft) and we automatically adjust other objects distance based on main subject size and other objects relative positions. This actually seems not depend on image viewing distance - our brain corrects this away :) Tom likely objects this?
And this may explain, why in some images we see 'telephoto compression' and in some images not - the later images likely don not have any objects, where we can make automatic assumptions about their distance and/or size. Somewhere in one Tom perspective thread were presented photos of two objects - we could look at each one (independently) and could not see compression so easily - not enough context. Side by side (and with author comments) 'compression' effects are visible.
-
@ArvoJ has written:
Back to perspective. I think that we see 'distortion' in the cases when we assume some distance to object and in reality it is taken from very different distance. (Same for object sizes.) Like full-size people images - we assume they have photographed from distance 3-6m (10-20ft) and we automatically adjust other objects distance based on main subject size and other objects relative positions. This actually seems not depend on image viewing distance - our brain corrects this away :) Tom likely objects this?
Why would I object to that? Obviously, our perception of what we are looking at depends greatly on the context. Depth perception depends on a very large number of cues that may (or may not) be present in the image. Many optical illusions (such as the three vans illusion that was discussed recently in dpreview) occur when different cues appear to be contradictory.
Perspective is just one cue that helps with depth perception (although often a very important one). I would never claim that depth perception depends on perspective alone, let alone just on the angular size of familiar objects which is the only thing that changes when just the viewing distance changes.
I am still very puzzled about what Andrew really thinks. He persistently avoids giving a precise description of what he thinks "telephoto compression" is and how it occurs, yet he very confidently claims that the explanations given in the Manual of Photography and elsewhere are all wrong.
-
@ArvoJ has written:
Back to perspective. I think that we see 'distortion' in the cases when we assume some distance to object and in reality it is taken from very different distance. (Same for object sizes.) Like full-size people images - we assume they have photographed from distance 3-6m (10-20ft) and we automatically adjust other objects distance based on main subject size and other objects relative positions. This actually seems not depend on image viewing distance - our brain corrects this away :) Tom likely objects this?
Tom is actually very close, but is yet to make that conceptual leap and question the base assumptions we make without evidence.
A Brief History of Perspective..
We are born.
We learn to interpret and navigate the space we occupy, we have a lot of practice and become exceptionally good at it. The real world becomes a stable and constant place. We believe we have an absolute and complete understanding because it remains consistent.
We learn maths which describes the absolute nature of the space we occupy.
Because the maths describes the absolute nature of the space and we have an absolute understanding we believe that they are one and the same with an incredible amount of inertia and use our langauge of maths to quantify and label our understanding of the space we occupy.
But the space that pure mathematical perspective describes, as seen by the camera and projected on the back of the retina, is actually one of constant shifting distortion. Yes, it's an absolute description, but that doesn't make it an absolute space.
The reason we have a constant understanding of the space we occupy is simply because the brain maintains consistency of understanding over the absolute maths. It basically means it distorts things so our understanding remains consistent. This is the nature of optical illusion, as you say deliberately introducing a conflict, and so the cracks become visible and the difference between the absolute world and our consistent understanding become obvious.
But which is better? The real world of pure mathematical geometry is a stable place for numbers but an ever shifting and confusing place for humans. Our understanding actually represents a far more accurate and stable overview of the true shapes of objects, but we get there purely by empirical means, without numbers.
Comparing angles and sizes in images with a human eye and relating that to geometry to explain how we see perspective in images is, to be blunt, nonsense. If you could see the difference between the perspective geometry describes and our actual perception of that space you'd realise immediately that is more than just trying to bang a square peg in a round hole.
@TomAxford has written:I am still very puzzled about what Andrew really thinks. He persistently avoids giving a precise description of what he thinks "telephoto compression" is and how it occurs, yet he very confidently claims that the explanations given in the Manual of Photography and elsewhere are all wrong.
Actually I didn't, I quite categorically remember stating that I agreed completely with them. But don't take my word, it's in black and white on this very site...
What I disagreed with was your interpretation that used the term exact same.
-
Suppose I take a photo of two objects against a completely uniform white background. Object A is at a distance of 10 (in whatever units you like) from the camera and object B is at a distance of 20 (in the same units). The photo is taken with a 500mm lens.
Then I take a second photo with object A at distance 1 and object B at distance 2; this time using a 50mm lens. The size of object A will be the same in both photos. The size of object B will also be the same in both. The positions of A and B relative to the camera are assumed to be consistent with their positions in the first photo.
So, our perception of depth in both photos will necessarily be the same (provided that the only thing in the photos from which we can judge depth is the size of the two objects).
In other words, the photo with a 500mm lens has the same apparent perspective as a photo with a 50mm lens and with all distances from the camera reduced to one tenth of their original values. This is another way of describing telephoto compression. It does not involve looking at the photos by eye. They could instead be analysed digitally with software. How our eyes work does not come into it..
-
[deleted]
-
@JACS has written:
Now, imagine using an UWA from the same point of view, where you used the 500mm lens. The "software perception" would still be the same.
The image of object A would not be the same size as in the 500mm lens. So the software perception would not be the same.
-
[deleted]
-
@TomAxford has written:
In other words, the photo with a 500mm lens has the same apparent perspective as a photo with a 50mm lens and with all distances from the camera reduced to one tenth of their original values.
No.
Absolutely no by the maths of pure image geometry alone. When rendering 3D scenes on a camera sensor foreshortening is a function of distance alone and is completely independent of focal length. the object at 10x the distance will show far more foreshortening.
Your opening argument in the OP (your bold):
@TomAxford has written:However, the perspective seen by the viewer of a photograph also depends on the viewer's position (relative to the image). Photographs are usually made to be viewed and any comprehensive discussion of perspective must include the viewer's viewpoint as well as the camera's viewpoint. This has been known for a very long time and at least back to the theories of perspective developed in the fifteenth century.
I will say this one more time, but I feel confident that you will still fail to grasp the meaning.
We do not see pure geometrical/mathematical perspective through human eyes.
So, what is the pure geometrical and mathematically correct appearance of a distant object?
Foreshortened
How that is rendered by pure geometry and correct maths onto a 2D plane?
Foreshortened
How is that 2D image rendered by pure geometry and correct maths to the back of the retina?
Exact copy of the original.
What we see when we view the image with a human eye?
Highly dependent on viewing position but generally accepted that we will normally see a distortion of the perspective.
Conclusion?
There is only one possible conclusion; we do not see the pure geometrical or correct mathematical perspective when we view images because if we did we would always see the same consistent foreshortened. The absolute truth is that the human visual system never sees pure geometrical or mathematically correct perspective
So it then becomes painfully obvious that you can't look at images and relate what you see to the pure geometry of image formation. If you did you would end up scrabbling around and making ever more nonsensical statements that contradict yourself, observation and pure geometry while still trying to bang that square peg in a round hole.
We see telephoto compression in images because we see those objects out of the context of their normal distance. We then make errors of judgement and misinterpret their perspective. The mathematically correct pure geometric perspective remains both constant and correct in an image, there is no misinterpretation in geometry, only in viewing. So you can't discuss it without including human perception.
This is getting so bizarre! All of the above must be plainly obvious??
-
@Andrew564 has written:@TomAxford has written:
In other words, the photo with a 500mm lens has the same apparent perspective as a photo with a 50mm lens and with all distances from the camera reduced to one tenth of their original values.
No.
Absolutely no by the maths of pure image geometry alone. When rendering 3D scenes on a camera sensor foreshortening is a function of distance alone and is completely independent of focal length. the object at 10x the distance will show far more foreshortening.
Objects A and B are flat objects. All of object A is at the same distance from the camera. So there is no foreshortening as it is of zero depth already.
If you want to consider an object in 3D, then take object A to be its front face and object B to be its rear surface (with nothing visible in between in this very simple example). The foreshortening is then equivalent to the change in distance between A and B in the two photo situations.
You can take a more realistic object if you like, but then every visible point on the object will need to be moved to one tenth the distance for photo 2.
@Andrew564 has written:We do not see pure geometrical/mathematical perspective through human eyes.
I have never said that we do. Perspective is a mathematical model to explain how the shapes and sizes of objects change when we project a 3D scene to a 2D image and then when the 2D image is viewed from a specified point (relative to the image).
I say "viewed" but that does not necessarily mean through human eyes. You could instead take a photo of it (from the specified point) or use machine vision to view it and interpret it.
Human vision is not an essential part of perspective. The same theory of perspective applies when photographs are analysed by machine.
@Andrew564 has written:We see telephoto compression in images because we see those objects out of the context of their normal distance. We then make errors of judgement and misinterpret their perspective.
What do you mean by "out of the context of their normal distance"? What errors of judgement are you referring to? Can you give a simple example, please?
-
@TomAxford has written:
Objects A and B are flat objects. All of object A is at the same distance from the camera. So there is no foreshortening as it is of zero depth already.
So...
@TomAxford has written:This is another way of describing telephoto compression.
Involving 2D objects which will display no compression either geometrically or perceptually?
But:
@Andrew564 has written:We do not see pure geometrical/mathematical perspective through human eyes.
And that includes your latest example, the relative sizes are not preserved in human vision, it's called size constancy scaling.
And:
@Andrew564 has written:We see telephoto compression in images because we see those objects out of the context of their normal distance. We then make errors of judgement and misinterpret their perspective. The mathematically correct pure geometric perspective remains both constant and correct in an image, there is no misinterpretation in geometry, only in viewing. So you can't discuss it without including human perception.
So the effect of telephoto compression doesn't exist in the maths...
It's still not registering.
Is it just me?
@TomAxford has written:What do you mean by "out of the context of their normal distance"? What errors of judgement are you referring to? Can you give a simple example, please?
No, I don't think I could make it simple enough to make any difference. There is enough information in this thread already.
There is nothing wrong with Ansel Adams' theory.
-
I'll stand by what I have said already. I think time will be the ultimate judge of who is right. Or perhaps we are both wrong. It seems unlikely that we are both right!
-
@TomAxford has written:
I'll stand by what I have said already. I think time will be the ultimate judge of who is right. Or perhaps we are both wrong. It seems unlikely that we are both right!
Ah, but I'm not the one trying to describe an effect that doesn't exist in pure geometry and only exists when we view images, entirely by the pure geometry that we don't see and the complete exclusion of human perception.
Besides, time was ticking before the start of the conversation and is pretty far along the road to being a judge already. But probably not so much on photo tutorial websites!
😀
-
@ArvoJ has written:@Andrew564 has written:
The front and back of our table here are exactly the same size, and so the two side are exactly parallel, and so the opposite angels are also exactly the same. This is the geometrical truth of the image and the truth of the photo and how it is mapped to the back of the retina.
Maybe I misunderstand you, but IMO this is not geometrical truth of the image. You could get such image only by telecentric lens, which geometrically places center of perspective into (minus) infinity (in other words, makes focal length infinite). Using pinhole or any usual lens, you will get quite different image - sides not parallel and back side shorter.
The table will be approaching that look at a long enough distance - where the 'telephoto compression' becomes apparent.
-
@Andrew564 has written:
The front and back of our table here are exactly the same size, and so the two side are exactly parallel, and so the opposite angels are also exactly the same. This is the geometrical truth of the image and the truth of the photo and how it is mapped to the back of the retina.
Looks similar to an Isometric projection whereby the edges of the table are the same size as their opposites, i.e. no perspective involved.
en.wikipedia.org/wiki/Isometric_projection
upload.wikimedia.org/wikipedia/commons/9/93/Comparison_of_graphical_projections.svg