I see a London (English) Bond with some fairly poor pointing work, but it was my trade and I'm not really seeing past it, (especially the poor pointing...) 😖
-
-
It's a good example.
Up close I see the obtuse angle. I can force my mind to see 90 degrees but it takes some effort.
It is interesting to watch the effect moving in from about half the cop to close. Even at 1/2, I see an angle > 90. It doesn't jump out but it's there.
-
[deleted]
-
At full size I see an obtuse angle for the corner, downsized to a thumbnail I see a normal 90 degree corner. If you keep the same viewing position, then downsizing has the same effect as increasing your viewing distance when the size remains the same.
If you can't see it, that doesn't mean that others can't. Depth perception is something that we learn to do from long experience.
-
Now I have read the OP in which this photo was first posted, and skimmed through the article on geometry and perspective. I do not doubt the maths.
The photo is not a great example, as in I don't think that everybody will see what you are trying to demonstrate. When we view this from a distance in front of the centre of perspective we see an obtuse angle. This is the correct geometric perspective of the corner viewed from the camera position and the correct geometric representation of that on a 2D plane.
If we view from the centre of perspective we understand the true shape of the object as being 90 degrees, even through the actual angle in the image is still the same.Now what I've been trying to explain all along is that the pure geometry of the image as projected on the back of the retina and the 3D understanding of actual real shape are not the same thing. It takes an extra layer of processing to get from one to the other. One of the processes the brain uses to convert that retinal image into a 90 degree corner (and form an understanding of correct 3D shape from 2D information) is not by maths but by actually changing the shape of the object. This prohibits you from reverse engineering the maths of image formation and using it as a direct explanation as to how we form a 3D understanding from a 2D image. It also shows that when we view the real world or an image from the centre of perspective we are at the one point where our vision fails to see the pure geometry and instead sees the understanding of actual shape.
As to the article. Well this thread has demonstrated very correctly that geometric perspective as displayed in photos is highly dependent on viewing distance, in fact to such an extent as to ensure that you almost never see the correct perspective in images. I'm not saying artists don't use linear perspective, just that they don't use it in the "pure" form. Just like artists don't go round bumping into walls (or become abstract impressionists) because they flunked maths and so can't see perspective very well, they do both generally because they are drunk. 😋
Also remember that though the Renaissance was the pinnacle of realism at the time it doesn't carry the same impact against the images that are now commonplace in the modern world.
-
Here is another image to test your depth perception. (Please view it from a distance of about 3 to 5 times the length of the diagonal)
Look at the nearer corner (on the right) of the building. Does the angle between the two walls appear to be (1) 90 degrees, (2) less than 90 degrees, or (3) greater than 90 degrees?Another interesting question to consider: Think of the plane defined by the wall of the building that we can see. Can you estimate which point in that plane is closest to the camera? In other words, the point from which a line drawn to the camera is perpendicular to the plane. Where do you judge that point is located?
(The centre of perspective of the image above is at a distance of 0.42 times the diagonal)
-
Well, of course they are not the same thing. The geometry of the image as projected onto the 2D photograph is not the same as the 3D geometry of the object being photographed. The geometry of the image on the retina will be different yet again.
I'm not trying to explain how our depth perception works. I agree that it is a very interesting question, but it is not necessary to address that question when explaining perspective.
When we say that we look at an image from closer than the centre of perspective and see "telephoto compression", that simply means that what we see looks like a real scene in which everything has been compressed towards the viewer.
In other words, if you were able to wave a magic wand and suddenly compress the real scene, then what you would see from the camera position would be like what you see when viewing the original photo from closer than the CoP. Mathematics can easily show this to be the case. The maths tells you what directions the light rays come from. What the maths doesn't tell you is whether the viewer can perceive depth in that scene (when viewed from a single fixed point, the camera position). If the viewer can perceive depth in a monocular view of the real scene, then he or she can probably also perceive depth in a view of the photograph (although many people do seem to find it difficult to get beyond their knowledge that they are looking at a 2D photograph).
When we view a photograph from closer than the CoP, the light rays from a small object in the photograph enter your eye from the same direction as the light rays enter your eye from the real object if everything in the scene is compressed towards the viewer. The closer the viewer is to the photograph, the more the real scene must be compressed for it to look the same as the photograph.
-
[deleted]
-
I still can't help thinking that we're still missing the fundamental and simple point here.
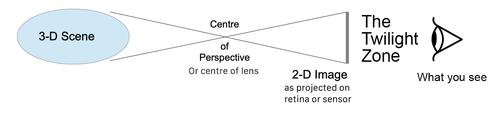
The image of the real world projected on the retina, like the one projected on a 2D sensor obeys the maths of pure geometry,
Is not the same as/does not equal
The image you see "with your eyes".
There is a layer of processing, lets call it "The Twilight Zone" because of the symmetrical meaning it conjurers, and call the one rule of TTZ "light does not travel in straight lines through TTZ.
Because that layer of processing includes things like Constancy Scaling it does in a very real sense mean that light doesn't travel in straight lines through TTZ.
So if you were to ray-trace from "what you see" through the centre of perspective to the real world it would fail to line up with the image projected on the back of the retina, and so would contradict the maths of geometry.
Telephoto compression only happens when we look at photos of distant objects, we never see it in other photos.
Foreshortening, or compression is the mathematical and geometrical fact of how distant objects are rendered on the retina/camera sensor.
Again you ray-trace directly from/to what you see, an imaginary space. And again the maths doesn't tell you anything of the sort. The maths only tells you what the retinal image should be, it fails to describe the "what you see" because of TTZ, so using geometry to describe "what you see" means that by very definition it must contradict the retinal image and therefore must also contradict geometry. And because you keep using "what you see" as the true baseline and relate that directly to geometry you are off base mathematically.
I think this is so wrong, telephoto compression and wide angle distortion are the function of camera to subject distance alone, the proof, and challenge, is simple:
If the above statement is correct then you will only see "telephoto compression" in photos of more distant objects viewed from the wrong distance.
And you will only see "wide angle distortion" in photos of close objects viewed from the wrong distance.
These two are not reversible with viewing distance.
If you are correct then you can show me a solid example where this is reversed with viewing distance.
My explanation is here:
-
Light behaves according to the laws of physics, which are well understood. The laws of physics and mathematics apply right up till the light hits the retina. After that it is reasonable to call it "the twilight zone". However, the twilight zone does not apply before the light enters the eyes.
That is simply not true. The image projected onto your retina follows the normal laws of geometry. It is after that that the brain takes over and we are into what you have dubbed "the twilight zone".
No, telephoto compression can happen with any photo, if viewed from closer than the CoP. However, we only see telephoto compression in images that contain familiar objects whose size can be used to help us judge distance. Of course, we can be deceived in many ways. For example, the Ames Room: we assume that it is a normal room with rectangular sides and a level floor, whereas in fact the sides are not rectangular and the floor isn't level, so our depth perception reaches incorrect conclusions when it assumes that the sides are rectangular and the floor is level as in a normal room.
Foreshortening is not the same thing as compression. Foreshortening is the change in aspect ratio caused by viewing a flat object at an angle. A photograph taken from the same position will show the same foreshortening as seen by the eye (provided the camera and the eye are at the same viewing position).
Telephoto compression occurs when a photograph is viewed with a greater angle of view (from one side of the photo to the other side) than that of the camera when the photo was taken.
This is incorrect. As I said before, light obeys the usual laws of physics until it hits the retina of the eye.
The rest of your comments that follow from these, are also incorrect.
It is not that easy to find a single photograph that will show both. A wide-angle photo is needed to easily show wide-angle perspective distortion, but it will not have sufficient resolution to enable it to be enlarged sufficiently to easily show telephoto compression.
To my mind, the easiest way to demonstrate that wide-angle perspective distortion and telephoto compression are the converse of each other is to use a telescope (or monocular). Look through the telescope in the usual way and you will often see telephoto compression (everything looks much closer). Look through the telescope backwards and you will often see wide-angle perspective distortion (everything looks much further away).
-
Again I think you miss the point.
Here you link what you see directly to maths and the maths directly to light rays. Again:
You can only directly link the retinal image with the geometry of image formation. And as "what you see" by definition is a different image than the retinal one any maths that links directly to it therefore cannot also follow the same maths of geometry, because it cannot by definition describe an image different to the retinal image and still be correct at the same time. So your statement above must also be incorrect.
It's quite simple, but you keep treating "what you see" as the retinal image and keep relating it directly to image geometry.
Why not? It is easy to find images that display telephoto compression and equally easy to find images that display wide angle distortion. So why can't you find one that doesn't fit my exact definition? I've nailed my colours to the mast and allowed you anything that falls outside it. It doesn't have to be both. By your theory a UWA shot viewed from normal distance should also show expansion of distant objects because they are viewed at a distance behind the centre of perspective. Just sayin'.
Doesn't work. They look further away but the distance between the distant objects is not expanded or stretched, and the definition I'm using is a simple one: Wide angle distortion is where the distance between objects or even the appearance of the depth of an object is stretched, telephoto compression is where it appears compressed.
-
Andrew, you are shooting at paper tigers. It is a commonly used distraction technique by those who have nothing constructive to add to the discussion: attack your opponents for statements they haven't actually made. I have never said that our brains interpret the signals from our eyes in terms of geometry.
Please read carefully what I wrote, think about it and try to understand it. I am getting really tired of you repeatedly criticising me for something I have never said and do not believe.
If you look backwards through an 8x telescope, everything looks approximately 8 times further away. An object 1m away appears to be 8m away, an object 2m away appears to be 16m away. The distance between the two objects is 1m, but it appears to be 8m when looking backwards through the telescope. It's just the same as zooming out to an UWA shot compared to zooming back with your feet - they are not the same thing.
@Andrew564 has written:By your theory a UWA shot viewed from normal distance should also show expansion of distant objects because they are viewed at a distance behind the centre of perspective. Just sayin'.
And it does. If you take an UWA shot of mountains that are a mile away, then they will appear to be much further away when the photo is viewed normally. I rarely use UWA lenses, so I do not have any examples to hand, but an online search will find plenty (e.g. here). Of course, unless you are familiar with that particular scene, you will not know if the mountains look further away than they actually are!
-
@TomAxford has written:
I think this is a reasonable example that shows both compression and wa distortion. I have to move back quite a way to see wa distortion but there is a point beyond which it is apparent to me.
Taken from this post earlier in the thread
dprevived.com/t/the-ansel-adams-fallacy-true-perspective-depends-only-on-the-camera-to-subject-distance/5326/post/70457/The good thing to do (for me at least) is to stand back where I see wa distortion. Then move forwards through the cop to where telephoto compression is apparent, observing the change along the way.
-
@TomAxford has written:@Andrew564 has written:
Here you link what you see directly to maths and the maths directly to light rays.
Andrew, you are shooting at paper tigers. It is a commonly used distraction technique by those who have nothing constructive to add to the discussion: attack your opponents for statements they haven't actually made. I have never said that our brains interpret the signals from our eyes in terms of geometry.
Please read carefully what I wrote, think about it and try to understand it. I am getting really tired of you repeatedly criticising me for something I have never said and do not believe.
Still the penny doesn't drop. So what does this mean then?
@TomAxford has written:...then what you would see from the camera position would be like what you see when viewing the original photo from closer than the CoP. Mathematics can easily show this to be the case. The maths tells you what directions the light rays come from.
I have repeatedly pointed out (google it yourself) that it is mathematical fact that we do not see pure geometry when we stand at the same position as the camera as the extra layer of processing distorts it. And yet you are specifically stating that "what you see" is proved by the maths. In theory there is a point where the retinal image should be the same, and the maths can absolutely demonstrate what you see is different, and as the nature of a 2D image is inherently different to the 3D scene there is no maths that says the two should look the same either. I think you doth assume too much...
But I give up, I throw in the towel on this one.
@TomAxford has written:If you look backwards through an 8x telescope, everything looks approximately 8 times further away. An object 1m away appears to be 8m away, an object 2m away appears to be 16m away. The distance between the two objects is 1m, but it appears to be 8m when looking backwards through the telescope. It's just the same as zooming out to an UWA shot compared to zooming back with your feet - they are not the same thing.
And if we look at a wide angle shot then we find that though true with the foreground the effect diminishes with distance as is predicted by geomerty, distant items are rendered foreshortened and as the distortion caused by human vision becomes less effective with distance we can say that what we see should be at least roughly equivalent to what geometry predicts, see below:
The foreground appears to extend but the background doesn't relative distances appear stable. I've tried it through bins but the image is too small, but I expect it is the same as geometry predics the wide angle shot to be, i.e. mathematically foreshortening is a function of distance and I do not see this reversed, I do not see the distances between the background objects extending.
@TomAxford has written:And it does. If you take an UWA shot of mountains that are a mile away, then they will appear to be much further away when the photo is viewed normally. I rarely use UWA lenses, so I do not have any examples to hand, but an online search will find plenty (e.g. here). Of course, unless you are familiar with that particular scene, you will not know if the mountains look further away than they actually are!
So telephoto compression is the effect where the distance between two objects appears compressed and wide angle distortion is when they look smaller? So your proof is that if I take a photo and move away from it wide angle distortion predicts that it will look smaller and this is dependant entirely on viewing distance.
Can't argue with that, so throwing in the towel here as well.
@Bryan has written:I think this is a reasonable example that shows both compression and wa distortion. I have to move back quite a way to see wa distortion but there is a point beyond which it is apparent to me.
I'm not seeing any wide angle distortion, as in the shapes are stretched in this image at any distance.
-
[deleted]
-
Most people would struggle to figure out the lens that took these pictures without EXIF data or other prior knowledge.


-
@JACS has written:
When there are enough cues in the scene, I would, of course. This is unmistakably an UWA image, and l know how it relates to the real scene:

Yes, quite often the amount of foreground and the appearance of the foreground are sufficient clues to the ultra-wide angle of view.
There are two aspects of wide-angle perspective distortion, which I should have clearly distinguished. First there is the extension of distances away from the camera (the inverse of telephoto compression, which is the compression of distances away from the camera). Second, there is the distortion of shapes when they are projected at an extreme angle onto a flat image (e.g. a sphere appears not as a circle but as an oval shape). The second is often much easier to detect than the first, but it does not occur in the centre of the image.
-
@TomAxford has written:@JACS has written:
When there are enough cues in the scene, I would, of course. This is unmistakably an UWA image, and l know how it relates to the real scene:

Yes, quite often the amount of foreground and the appearance of the foreground are sufficient clues to the ultra-wide angle of view.
There are two aspects of wide-angle perspective distortion, which I should have clearly distinguished. First there is the extension of distances away from the camera (the inverse of telephoto compression, which is the compression of distances away from the camera). Second, there is the distortion of shapes when they are projected at an extreme angle onto a flat image (e.g. a sphere appears not as a circle but as an oval shape). The second is often much easier to detect than the first, but it does not occur in the centre of the image.
You keep conflating different subjects. First it's perspective versus viewing condition, now it's perspective versus projection. Circles appear as ovals on the edge of a rectilinear image because of that type of projection. Such is not the case with all projections.